Задача 1 (Т-06, 46) Укажіть номер фужера, у який можна налити найбільше рідини. 1 3 2
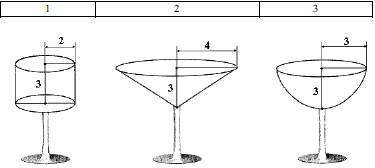
Розв'язання: Знайдемо об'єм тіл, які можна вмістити в фужери. Перше- циліндр з радіусом основи 2 та висотою 3. Об'єм циліндра рівний
V=Pi*2*2*3=12*Pi.
Другий – конус, його об'єм рівний
V=1/3*Pi*4*4*3=16*Pi.
Третій фужер це півсфера радіусом 3.
Об'єм півсфери рівний
V=Pi*3^3/2=13,5*Pi.
Порівнявши об'єми фужерів приходимо до висновок, що у 2 можна налити найбільше рідини.
Розв'язання: Знайдемо об'єм тіл, які можна вмістити в фужери. Перше- циліндр з радіусом основи 2 та висотою 3. Об'єм циліндра рівний
V=Pi*2*2*3=12*Pi.
Другий – конус, його об'єм рівний
V=1/3*Pi*4*4*3=16*Pi.
Третій фужер це півсфера радіусом 3.
Об'єм півсфери рівний
V=Pi*3^3/2=13,5*Pi.
Порівнявши об'єми фужерів приходимо до висновок, що у 2 можна налити найбільше рідини.
Задача 2 Через вершину конуса з радіусом основи 4 см проведено площину, що перетинає його основу по хорді, яку видно з центра основи конуса під кутом 120°, а з вершини конуса - під кутом 90°. Обчисліть площу перерізу, у см2.
Задача 3 . Бічне ребро піраміди розділене на чотири рівні частини й через точки ділення проведені площини, паралельні основі. Площа основи дорівнює 400 
. Знайдіть площі перетинів.
. Знайдіть площі перетинів.
Розв'язання. Перетини подібні основі піраміди з коефіцієнтами подобія 
, 
і 
. Площі подібних фігур відносяться як квадрати лінійних розмірів. Тому відносини площ перетинів до площі основи піраміди є 
, 
і 
. Отже площі перетинів рівні
, 
.
Розв'язання. Бічні грані усіченої піраміди — трапеції з однією і тією самою верхньою основою а, нижньою b і висотою (апофемою) l. Тому площа однієї грані дорівнює —
. Площа всіх граней, тобто бічна поверхня, дорівнює — 
, де n — число вершин у основі піраміди, an і bn — периметри основ піраміди.
, і . Площі подібних фігур відносяться як квадрати лінійних розмірів. Тому відносини площ перетинів до площі основи піраміди є , і . Отже площі перетинів рівні , .Розв'язання. Бічні грані усіченої піраміди — трапеції з однією і тією самою верхньою основою а, нижньою b і висотою (апофемою) l. Тому площа однієї грані дорівнює —
. Площа всіх граней, тобто бічна поверхня, дорівнює — , де n — число вершин у основі піраміди, an і bn — периметри основ піраміди. |
| Рис. 4 |
3адача 4. Доведіть, що бічна поверхня правильної усіченої піраміди дорівнює добутку півсуми периметрів основ на апофему.
Розв'язання. Проведемо з вершини S тетраедра висоти SA, SB, SC його граней, що сходяться в цій вершині, і висоту SO тетраедра (рис. 4). Якщо ребро тетраедра позначити через а, то висоти граней будуть рівні 
. З рівності висот SA, SB, SC слідує рівність відрізків OA, OB, OC. А вони перпендикулярні сторонам трикутника в основі тетраедра (по теоремі про три перпендикуляри). Звідси слідує, що точка О є центром окружності, що вписана в основу тетраедра. Отже, відрізки OA, OB, і OC рівні 
. Позначимо через 
двогранний кут при ребрі, що містить точку А. Тоді 
.
. З рівності висот SA, SB, SC слідує рівність відрізків OA, OB, OC. А вони перпендикулярні сторонам трикутника в основі тетраедра (по теоремі про три перпендикуляри). Звідси слідує, що точка О є центром окружності, що вписана в основу тетраедра. Отже, відрізки OA, OB, і OC рівні . Позначимо через двогранний кут при ребрі, що містить точку А. Тоді .
Очевидно, двогранні кути при інших ребрах тетраедра такі ж по величині.
Немає коментарів:
Дописати коментар